这节课主要讨论一下机器学习中过拟合的问题。
What is Overfitting?
Overfitting
什么是过拟合?首先来看一下之前介绍过的 VC 曲线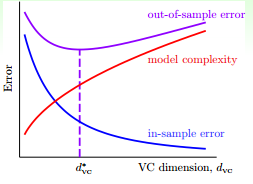
随着 $d_{\text{VC}}$ 的变大,$E_{\text{in}}$ 逐渐变小,而 $E_{\text{out}}$ 先变小再变大。我们把 $E_{\text{out}}$ 最小位置所对应的 $d_{\text{VC}}$ 称为 $d_{\text{VC}}^{*}$,于是把曲线分成了两部分。
- 在 $d_{\text{VC}}^{*}$ 左边部分,$E_{\text{in}}$ 与 $E_{\text{out}}$ 都比较大,说明模型对样本的拟合较差,这种情况称为欠拟合。
- 在 $d_{\text{VC}}^{*}$ 右边部分,随着 $d_{\text{VC}}$ 的变大,$E_{\text{in}}$ 逐渐变小,而 $E_{\text{out}}$ 却逐渐变大,说明模型对训练样本拟合得很好,但是泛化能力较差,这种情况称为过拟合。
Cause of Overfitting
发生过拟合的原因主要有:
- 使用过于复杂的模型,$d_{\text{VC}}$ 过大;
- 数据存在噪声;
- 训练样本数过少。
The Role of Noise and Data Size
Case Study
现在假设我们有两组数据,第一组数据由一个 10 阶的目标函数加噪声生成,第二组数据由一个 50 阶的目标函数生成。分别使用 2 阶以及 10 阶的多项式模型来学习这两组数据。
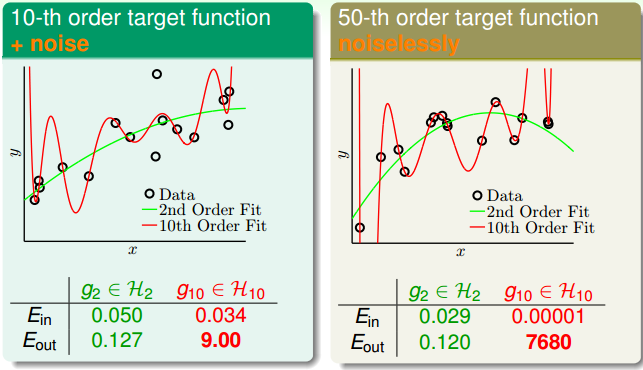
从上图可以看出,无论学习哪组数据,$E_{\text{in}}(g_2)$ 大于 $E_{\text{in}}(g_{10})$,而 $E_{\text{out}}(g_2)$ 小于 $E_{\text{out}}(g_{10})$。因此,对于这两组学习,可以说 $g_{10}$ 发生了过拟合。
Learning Curves Revisited
从学习曲线来看,两个模型的学习曲线如下: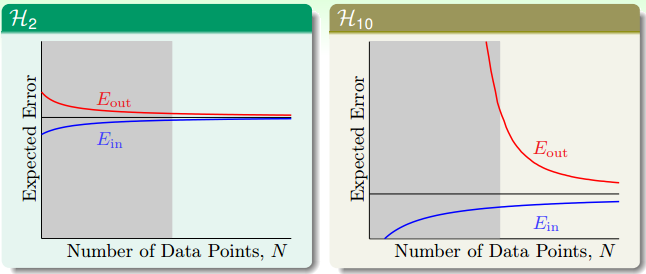
可见,当样本数目 $N$ 足够大时,两个模型会收敛,这时右边模型的 $E_{in}$ 与 $E_{out}$ 都会比左边的小。但是当样本数 $N$ 不够时,对右边模型来说,尽管 $E_{in}$ 很小,但是 $E_{out}$ 会特别大,这就是发生了过拟合。可以说是 $N$ 过小造成的,也可以说是 $d_{\text{VC}}$ 过大造成的。
The No Noise Case
第二组数据是由一个 50 阶的目标函数生成,没有加噪声。但是两个模型学习的结果仍然是,$\mathcal{H}_{10}$ 过拟合。这种情况可以这样解释:目标函数本身就很复杂,这本质上来讲也是一种噪声,我们称之为确定性噪声(Deterministic Noise),我们将在下面进行进一步解释。
Deterministic Noise
我们来探讨一下影响过拟合的一些因素。
Impact of Noise and Data Size
假设我们产生的数据分布由两部分组成:第一部分是目标函数 $f(\mathbf{x})$ 是一个 $Q_f$ 阶多项式,第二部分是服从高斯分布的随机噪声 $\epsilon$,其中方差是 $\sigma^2$。此外,数据样本数是 $N$。
$(N,\sigma^2)$ 与 $(N,Q_f)$ 对过拟合的影响可以表示成下图。其中,红色越深,代表过拟合程度越高,蓝色越深,代表过拟合程度越低。可以看出,$N$ 越小,$\sigma^2$ 越大,$Q_f$ 越大,越容易过拟合。我们把 $\sigma^2$ 成为随机噪声,$Q_f$ 称为确定性噪声。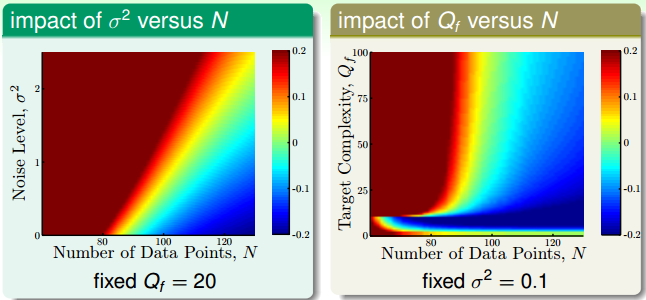
Deterministic Noise
确定性噪声可以这样来分析,当目标函数 $f$ 不在 $\mathcal{H}$ 的范围里的时候,我们无法从 $\mathcal{H}$ 中选到 $f$,(比如上面的例子,我们无法在 $\mathcal{H}_{10}$ 中选择出阶数为 50 的目标函数 $f$)。这种情况下,$\mathcal{H}$ 中的最优解 $h$ 与 $f$ 是存在一定差距中,这个差距就叫做确定性噪声。
确定性噪声对过拟合的影响与随机噪声大致一样。与随机噪声不同的是,确定性噪声取决于 $\mathcal{H}$,并且当给定 $\mathbf{x}$ 的时候,确定性噪声就确定下来了。
Dealing with Overfitting
有许多手段可以解决过拟合问题:
- start from simple model
- data cleaning/pruning
- data hinting
- regularization
- validation
下一讲将介绍其中的 regularization,尽情期待。


