Restriction of Break Point
上次我们说到,需要探究 “break point” $k$ 与 $m_\mathcal{H}(N)$ 之间的关系。回顾一下,$m_\mathcal{H}(N)$ 表示假设空间在 $N$ 个样本点上能产生的最大二分数量,$k$ 表示不能满足完全分类情形的样本点数。
让我们来探讨一下,当 $k$ 确定时,$m_\mathcal{H}(N)$ 的最大可能取值,下面使用一个例子来进行探讨。
Example: Break Point $k=2$
根据 break point 的定义
- 当样本数为 $N=1$ 时,需要满足样本完全二分的情况,因此 $m_\mathcal{H}(1) = 2^1 = 2$
- 当样本数为 $N=2$ 时,不可满足样本完全二分的情况,因此 $m_\mathcal{H}(2) < 2^2 = 4$,最多为 $m_\mathcal{H}(2)=3$
- 当样本数为 $N=3$ 时,同样不可满足样本完全二分的情况,因此 $m_\mathcal{H}(3) < 2^3 = 8$,但是由于 $m_\mathcal{H}(2)$ 已经存在上限 $m_\mathcal{H}(2)<4$,因此 $m_\mathcal{H}(3)$ 的值会有更严格的上限。根据实验可以得到 $m_\mathcal{H}(3) < 5$。
$k=2$ 时 $m_\mathcal{H}(3) < 5$ 的含义是:当样本数为 $N=3$ 时,假设空间最多有 $4$ 种分类结果,使得对任意 $k=2$ 个样本,不能满足完全分类的情形。
以上的分析比较晦涩难懂,我们使用图片重新说明一下。可以看到当只有 $1,2,3$ 种分类结果的时候,任意两个样本都不会出现完全分类的情形。当有 $4$ 种分类结果的时候,可能会出现有两个样本完全分类的情况,也可能不出现这种情况。而有 $5$ 种分类结果的时候,始终会出现有两个样本完全分类的情况。因此,二分类结果最多只能有 $4$ 种。




Bounding Function: Basic Cases
我们将刚才讨论的东西起一个名字,叫做 bounding function $B(N,k)$,表示当 break point 为 $k$ 的时候,$m_\mathcal{H}(N)$ 的最大可能的值。
那么经过前面的例子,我们可以得到一些结论:
- $k=1$ 时,$B(N,k)=1$(任意一个点都不能被完全分类,因此只能有一种分类结果)
- $k>N$ 时,$B(N,k)=2^N$(总共就 $N$ 个点,最多就 $2^N$ 种分类结果);
- $k=N$ 时,$B(N,k)=2^N-1$(减去一种分类结果,则任意 $N$ 个点不会被完全分类);
- $B(3,2)=4$(刚才的例子);
于是我们得到了下面这个表格:
$$
\begin{array}{c|lcr}&&&&k\\
B(N,k)&1&2&3&4&5&6&\cdots \\
\hline
1&1&2&2&2&2&2&\cdots\\
2&1&3&4&4&4&4&\cdots\\
3&1&4&7&8&8&8&\cdots\\
4&1&&&15&16&16&\cdots\\
5&1&&&&31&32&\cdots\\
6&1&&&&&63&\cdots\\
\vdots&\vdots&&&&&&\ddots
\end{array}
$$
Bounding Function: Inductive Cases
至此,我们已经解决了一半的问题。不过,表格里打问号的才是我们要讨论的重点,我们试着通过递推的方法得到这些值。
Dichotomies of $B(4,3)$
我们用计算机列举出 $B(4,3)$ 的所有可能,同时将这些结果重新排列,如下图所示: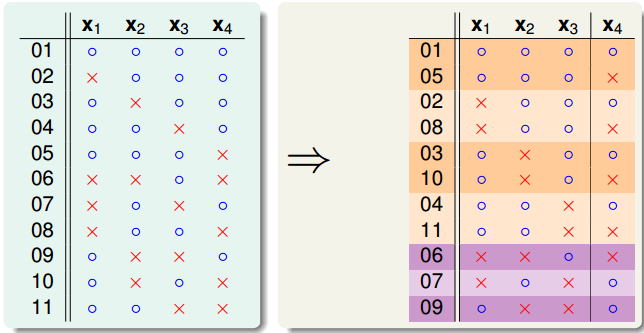
其中橙色的表示前 $3$ 个样本点成对出现,数量记为 $2\alpha$,绿色的表示前 $3$ 个样本点单独出现,数量记为 $\beta$,那么有 $B(4,3) = 2 \alpha + \beta$。
$B(4,3)$ 表示所有 $4$ 个样本点中,任意 $3$ 个都不会被完全分类。那么去掉第 $4$ 个样本,可以得到:
- $\alpha+\beta$ 中,前 $3$ 个样本点中的任意 $3$ 个不会被完全分类,$\alpha + \beta \le B(3,3)$;
- $\alpha$ 中,前 $3$ 个样本点中的任意 $2$ 个不会被完全分类,$\alpha \le B(3,2)$(因此第 $4$ 个点会被完全分类);
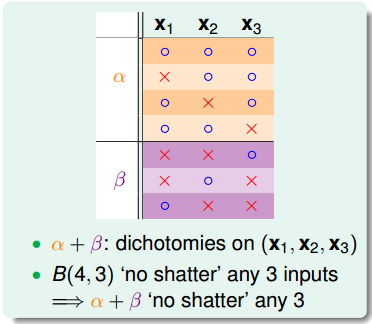

因此:
$$B(4,3) = 2\alpha+\beta=(\alpha+\beta)+\alpha\le B(3,3)+B(3,2)$$
推广到其他:
$$B(N,k)\le B(N-1,k)+B(N-1,k-1)$$
数学归纳法可以证明:
$$B(N,k) \leq \sum_{i=0}^{k-1} {N \choose i}$$
因此可以得到,当 break point $k$ 存在时
$$m_\mathcal{H}(N) \le B(N,k) \leq \sum_{i=0}^{k-1} {N \choose i}$$ $m_\mathcal{H}(N)$ 是 $N$ 的多项式函数。
Mathematical Induction
下面使用数学归纳法证明 $B(N,k) \le\sum_{i=0}^{k-1}{N \choose i}$
- $k=1$ 时,不等式恒成立,因此只讨论 $k \ge 2$ 的情形;
- $N=1$ 时,不等式成立;
- 假设 $N=No$ 时,不等式成立,下面证明 $N=No+1$ 时,不等式成立。
$$
\begin{aligned}
B(N_{o}+1,k) &\leq B(N_{o},k) + B(N_{o},k-1) \\\
&\leq \sum_{i=0}^{k-1}\binom{N_{o}}{i}+\sum_{i=0}^{k-2}\binom{N_{o}}{i} \\\
&=1+\sum_{i=1}^{k-1}\binom{N_{o}}{i}+\sum_{i=1}^{k-1}\binom{N_{o}}{i-1} \\\
&=1+\sum_{i=1}^{k-1}[\binom{N_{o}}{i}+\binom{N_{o}}{i-1}] \\\
&=1+\sum_{i=1}^{k-1}\binom{N_{o}+1}{i}=\sum_{i=0}^{k-1}\binom{N_{o}+1}{i}
\end{aligned}
$$
A Pictorial Proof
于是利用有限的 $m_{\mathcal{H}}(N)$ 来替换无限的 $M$,得到 $\mathcal{H}$ 遇到Bad Sample的概率上界:
$$\mathbb{P}_\mathcal{D}[BAD\ D]\leq 2m_{\mathcal{H}}(N)\cdot exp(-2\epsilon ^2N)$$
用更加精准的数学符号来表示上面的不等式:
$$\mathbb{P}[\exists h \in \mathcal{H}\text{ s.t. } |E_{in}(h)-E_{out}(h)|\gt \epsilon]\leq 2m_{\mathcal{H}}(N)\cdot exp(-2\epsilon ^2N)$$
但事实上上面的不等式是不严谨的,因为 $m_{\mathcal{H}}(N)$ 描述的是 $\mathcal{H}$ 作用于数据量为 $N$ 的资料 $\mathcal{D}$ 有效的方程数,因此 $\mathcal{H}$ 当中每一个 $h$ 作用于 $\mathcal{D}$ 都能算出一个 $E_{in}$ 来,一共能有 $m_{\mathcal{H}}(N)$ 个不同的 $E_{in}$,是一个有限的数。但在out of sample的世界里(总体),往往存在无限多个点,平面中任意一条直线,随便转一转动一动,就能产生一个不同的 $E_{out}$ 来。$E_{in}$ 的可能取值是有限个的,而 $E_{out}$ 的可能取值是无限的,无法直接套用union bound,我们得先把上面那个无限多种可能的 $E_{out}$ 换掉。
下面涉及到许多数学公式,先挖个坑,有时间补上。


