这节课主要介绍使用线性模型来解决分类问题。
Linear Models for Binary Classification
Linear Models Revisited
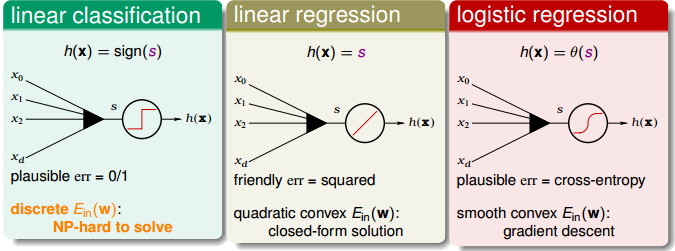
之前我们介绍了三种线性模型,分别是 Linear Classification,Linear Regression 以及 Logistic Regression。
这几个模型,都是对样本特征进行加权,得到一个分数 $$s = \mathbf{w}^T \mathbf{x} $$ 再通过 $s$ 构成预测函数 $h(\mathbf{x})$ 以及误差函数 $\text{err}(s,y)$。
- Linear Classification
$$ \begin{aligned}
&h(\mathbf{x}) = \text{sign}(s)\\
&\text{err}(h,\mathbf{x},y) = \big[\big[ h(\mathbf{x}) \neq y \big]\big]\\
&\text{err}(s,y) = \big[\big[ \text{sign}(s) \neq y \big]\big] = \big[\big[ \text{sign}(sy) \neq 1 \big]\big]\\
\end{aligned} $$ - Linear Regression
$$ \begin{aligned}
&h(\mathbf{x}) = s\\
&\text{err}(h,\mathbf{x},y) = \big( h(\mathbf{x}) - y \big)^2 \\
&\text{err}(s,y) = (s-y)^2 = (ys - 1)^2
\end{aligned} $$ - Logistic Regression
$$ \begin{aligned}
&h(\mathbf{x}) = \theta (s)\\
&\text{err}(h,\mathbf{x},y) = - \text{ln} h(y \mathbf{x})\\
&\text{err}(s,y) = \text{ln} \big( 1+\text{exp}(-ys) \big)\\
\end{aligned} $$
这三种模型的 error function 都引入了 $ys$,我们可以理解成,$ys$ 是表示分类准确率的一个分数,$ys$ 越大,分类准确率越高。
Visualizing Error Functions
图形化表示这三者的 error function,如下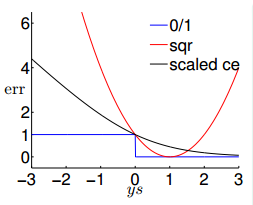
其中我们将 Logistic Regression 的 error function 进行了一个缩放。
Theoretical Implication of Upper Bound
可以看出,$\text{err}_{\text{sqr}}$ 与 $\text{err}_{\text{scaled ce}}$ 都是 $\text{err}_{\text{0/1}}$ 的 upper bound 函数。
$$ \text{err}_{\text{0/1}}(s,y) \leq \text{err}_{\text{SCE}}(s,y) = \frac{1}{\text{ln}2} \text{err}_{\text{CE}}(s,y)
$$ 可以推出 $$
\begin{aligned}
&E_{\text{in}}^{\text{0/1}}(\mathbf{w}) \leq E_{\text{in}}^{\text{SCE}}(\mathbf{w}) = \frac{1}{\text{ln}2} E_{\text{in}}^{\text{CE}}(\mathbf{w})\\
&E_{\text{out}}^{\text{0/1}}(\mathbf{w}) \leq E_{\text{out}}^{\text{SCE}}(\mathbf{w}) = \frac{1}{\text{ln}2} E_{\text{out}}^{\text{CE}}(\mathbf{w})\\
\end{aligned}
$$ 根据 VC 理论可以得到 $$
\begin{aligned}
&E_{\text{out}}^{\text{0/1}}(\mathbf{w}) \leq E_{\text{in}}^{\text{0/1}}(\mathbf{w}) + \Omega ^ {\text{0/1}}
\leq \frac{1}{\text{ln}2} E_{\text{in}}^{\text{CE}}(\mathbf{w}) + \Omega ^ {\text{0/1}}\\
&E_{\text{out}}^{\text{0/1}}(\mathbf{w}) \leq \frac{1}{\text{ln}2} E_{\text{out}}^{\text{CE}}(\mathbf{w}) \leq \frac{1}{\text{ln}2} E_{\text{in}}^{\text{CE}}(\mathbf{w}) + \Omega ^ {\text{0/1}}\\
\end{aligned}
$$
说明 $\text{err}_{\text{sqr}}$ 或者 $\text{err}_{\text{scaled ce}}$ 很小的时候,意味着 $\text{err}_{\text{0/1}}$ 也很小。因此,Linear Regression 和 Logistic Regression 都可以用来解决 Linear Classification 的问题。通常,我们使用 Linear Regression 得到 $\mathbf{w}_{0}$,再用 Logistic Regression 进行求解。
Regression for Classification
PLA,Linear Regression 以及 Logistic Regression 处理分类问题时,优缺点总结如下
- PLA:
优点:数据线性可分时,$\text{err}_{\text{0/1}}$ 可以降到最低;
缺点:数据非线性可分时,需要使用 Pocket 算法,较难最优化; - Linear Regression:
优点:最容易做最优化;
缺点:在 $ys$ 很大或很小时,Bound 是很宽松的; - Logistic Regression:
优点:较容易最优化;
缺点:在 $ys$ 是很小的负数时,Bound 是宽松的;
Stochastic Gradient Descent
Two Iterative Optimization Schemes
之前我们介绍过 PLA 以及 Logistic Regression,这两种算法都使用迭代的方法来更新参数的值
$$ \mathbf{w}_{t+1} = \mathbf{w}_{t} + \eta \ \mathbf{v}$$
- PLA 每次迭代只计算一个点,时间复杂度 $O(1)$
- Logistic Regression 每次迭代要对所有点都进行计算,时间复杂度 $O(N)$
下面介绍一种算法:随机梯度下降算法 (Stochastic Gradient Descent,SGD),可以提高更新参数的速度。
Stochastic Gradient Descent (SGD)
SGD 算法每次迭代只找到一个点,计算该点的梯度,作为我们下一步更新参数的依据。这样就保证了每次迭代的计算量大大减小,我们可以把整体的梯度看成这个随机过程的一个期望值。
- Stochastic Gradient
$\nabla_{\text{w}} \ \text{err}(\mathbf{w}, \mathbf{x}_n, y_n)$ with random $n$ - True Gradient
$\nabla_{\text{w}} \ E_{\text{in}}(\mathbf{w}) = {\underset{\text{random}\ n}{\epsilon}} \nabla_{\text{w}} \ \text{err}(\mathbf{w}, \mathbf{x}_n, y_n)$
于是,可以将 SGD 中梯度下降的方向理解成真实的梯度方向加上均值为零的随机噪声方向:
$${\text{stochastic gradient}} = {\text{true gradient}} + {\text{zero-mean noise directions}}
$$ 在运行足够多轮后,SGD 的效果与 GD 的效果是大致一样的。
下面对 SGD 做一个小结:
- 优点:计算量低,适用于大数据或者在线学习
- 缺点:每次迭代并不能保证按照正确的方向前进,不够稳定
PLA & SGD Logistic Regression
PLA 与 SGD Logistic Regression 这两种算法在参数更新上有相似之处
- SGD Logistic Regression
$$\mathbf{w}_{t+1} \leftarrow \mathbf{w}_{t} + \eta \cdot \theta(-y_n \mathbf{w}_t^T \mathbf{x}_n) (y_n \mathbf{x}_n)$$ - PLA
$$\mathbf{w}_{t+1} \leftarrow \mathbf{w}_{t} + 1 \cdot \big[\big[ y_n \neq \text{sign}(\mathbf{w}_t^T \mathbf{x}_n) \big]\big] (y_n \mathbf{x}_n)$$
可以把 SGD Logistic Regression 看成是 soft PLA:
- PLA:每次迭代只对分错的样本进行修正
- SGD Logistic Regression:每次迭代都会进行修正(不管分对分错)
- 当 $\eta = 1$ 且 $\mathbf{w}_t^T \mathbf{x}_n$ 时,PLA 相当于 SGD Logistic Regression
Multiclass via Logistic Regression
之前我们讨论的都是使用分类器解决二类别分类问题,接下来我们准备讨论使用分类器解决多类别分类问题。
我们举一个例子来进行讲解,需要将下图的图形分为正方形、菱形、三角形、星形四类:
一种策略是将 $k$ 分类问题转化为 $k$ 个二分类问题:是不是第 $i( i =1,2 \cdots k)$ 类,然后再根据这些问题的答案决定每个样本的类别,如下图所示。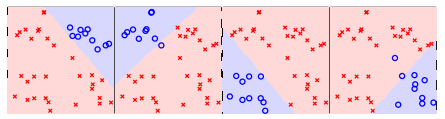
这种策略存在的问题是,可能出现分不了的情况,如某些区域同时被多个类判断为正(负)类。为了解决这个问题,可以改用软性分类器,即让上述的二分类问题输出概率而不是类别信息。
这种策略称为 One-Versus-All(OVA),是一种常用的多类别分类策略。
Multiclass via Binary Classification
上面介绍的 OVA 策略存在一个问题,当正负样本数不平衡的时候,会影响分类的性能,因此提出了另外一种策略。
在 OVO 策略下,每 2 个类别之间形成一个二分类问题,于是将 $k$ 分类问题转化为 $C_{k}^{2}$ 个二分类问题,然后再根据这些问题的答案决定每个样本的类别,如下图所示。
这种策略称为 One-versus-One(OVO),是一种常用的多类别分类策略。


