这一节主要介绍 Logistic Regression 算法。
Logistic Regression
Logistic Regression 是一个分类算法,主要用于二分类的情况,算法预测的是样本属于某个类别的概率,即 $h(\mathbf{x}) = P(+1 | \mathbf{x})$。
因为 $h(\mathbf{x})$ 表示的是一个概率值,为了使其范围在 0 到 1 之间,我们使用了 Logistic 函数
$$\theta(s) = \frac{1}{1+e^{-s}}$$ 于是 $$
h(\mathbf{x}) = \theta(\mathbf{w}^T\mathbf{x}) = \frac{1}{1+e^{-\mathbf{w}^T\mathbf{x}}}$$
将取值范围为负无穷到正无穷的 $\mathbf{w}^T\mathbf{x}$ 映射到了 0 到 1。
Logistic Regression Error
有了 $h(\mathbf{x})$ 之后,我们还需要找出 $E_{\text{in}}(\mathbf{w})$ 的表达式,在 Logistic Regression 算法中,$E_{\text{in}}(\mathbf{w})$ 是通过最大似然准则得到的。
首先介绍一下似然这个概念。假设我们有一笔数据 $$\mathcal{D}=\big\{ (\mathbf{x}_{1}, +1),\mathbf{x}_{2}, -1),\cdots,\mathbf{x}_{N}, -1), \big\}$$ 那么通过真实的函数 $f$ 得到这批数据的概率可以写成下面的表达式:
$$\text{probability}(f) = P(\mathbf{x}_1)f(\mathbf{x}_1) \cdot P(\mathbf{x}_2)(1-f(\mathbf{x}_2)) \cdots P(\mathbf{x}_N)(1-f(\mathbf{x}_N))
$$ 同理,通过预测函数 $h$ 得到这批数据的概率可以写成下面的表达式:
$$\text{likelihood}(h) = P(\mathbf{x}_1)h(\mathbf{x}_1) \cdot P(\mathbf{x}_2)(1-h(\mathbf{x}_2)) \cdots P(\mathbf{x}_N)(1-h(\mathbf{x}_N))
$$
我们的目标是要预测 $h$ 使它接近 $f$,而通常来说 $\text{probability}(f)$ 很大,所以我们可以最大化 $\text{likelihood}(h)$。这时意味着 $h$ 生成 $\mathcal{D}$ 的似然(或者说概率)很大,一定程度上可以说,$h \approx f$。
接下来的工作就是要最大化 $\text{likelihood}(h)$
$$g = \underset{h}{\text{argmax}} \ \ \text{likelihood}(h)
$$ 将常量 $P(\mathbf{x})$ 去掉,同时注意到 $1-h(\mathbf{x}) = h(\mathbf{-x})$,有
$$\text{likelihood}(h)
\propto \prod \limits_{i=1}^n h(y_n\mathbf{x}_n) = \prod \limits_{i=1}^n \theta(y_n \mathbf{w}^T_n\mathbf{x}_n)
$$ 取对数,并做一下相关变换,得到
$$\min_\mathbf{w} \frac{1}{N} \sum_{n=1}^{N} -\ln \theta(y_n \mathbf{w}^T \mathbf{x}_n)
$$ 即 $$ \min_\mathbf{w} \frac{1}{N} \sum_{n=1}^{N} \ \ln \left( 1 + \text{exp} ( -y_n \mathbf{w}^T \mathbf{x}_n ) \right)
$$ 因此,这就是 Logistic Regression 的损失函数
$$\text{err}(\mathbf{w}, \mathbf{x}, y) = \ln \left( 1 + \text{exp} ( -y_n \mathbf{w}^T \mathbf{x}_n ) \right)
$$ 称之为交叉熵损失函数。
Gradient of Logistic Regression Error
为了最小化损失函数
$$E_{\text{in}}(\mathbf{w}) = \frac{1}{N} \sum_{n=1}^{N} \ \ln \left( 1 + \text{exp} ( -y_n \mathbf{w}^T \mathbf{x}_n ) \right)
$$ 通常采取的方法是梯度下降法,如图所示:
为方便表示,我们使用 $\Box$ 表示 $\left( 1 + \text{exp} ( -y_n \mathbf{w}^T \mathbf{x}_n ) \right)$,使用 $\bigcirc$ 表示 $( -y_n \mathbf{w}^T \mathbf{x}_n )$。
那么求导过程如下:
$$\begin{aligned}
\frac{\partial E_{\text{in}}(\mathbf{w})}{\partial w_i}
&=\frac{1}{N} \sum_{n=1}^{N} \
\Big( \frac{\partial \ln (\Box)} {\partial \Box}\Big)
\Big( \frac{\partial (1 + \text{exp}(\bigcirc)) } {\partial \bigcirc} \Big)
\Big( \frac{\partial -y_n \mathbf{w}^T \mathbf{x}_n} {\partial w_i}\Big)\\
&=\frac{1}{N} \sum_{n=1}^{N} \
\Big( \frac{1}{\Box} \Big)
\Big( \text{exp}(\bigcirc) \Big)
\Big( -y_n x_{n,i} \Big)\\
&=\frac{1}{N} \sum_{n=1}^{N} \
\frac{\text{exp}(\bigcirc)} {1 + \text{exp}(\bigcirc)}
\big( -y_n x_{n,i} \big)\\
&=\frac{1}{N} \sum_{n=1}^{N} \
\theta(\bigcirc) \big( -y_n x_{n,i}\big)
\end{aligned}
$$ 于是
$$\nabla E_{\text{in}}(\mathbf{w}) = \frac{1}{N} \sum_{n=1}^{N} \ \theta \big( -y_n \mathbf{w}^T \mathbf{x}_n \big)
\big( -y_n \mathbf{x}_n\big)
$$ 我们的目标是使得 $\nabla E_{\text{in}}(\mathbf{w}) = 0$,这里可以分为两种情况
- 所有 $\theta(\cdot)$ 都为 $0$,这时表示所有 $y_n \mathbf{w}^T \mathbf{x}_n \gg 0$,说明线性可分
- 加权结果为 $0$,说明线性不可分
Gradient Descent
下面来讲一下梯度下降法,这是一种迭代的方法,通过不断的迭代来更新参数的值:
$$\mathbf{w}_{t+1} \leftarrow \mathbf{w}_{t} + \eta \mathbf{v}
$$ 其中 $\eta$ 表示的是步长,$\mathbf{v}$ 表示的是方向。
我们暂时假定步长是给定的,那么在每一次的迭代过程中,等价于求解下面的问题:
$$\underset{||\mathbf{v}=1||}{\text{min}} E_{\text{in}}(\mathbf{w}_t + \eta \mathbf{v})
$$ 当 $\eta$ 很小的时候,使用泰勒展开,有
$$E_{\text{in}}(\mathbf{w}_t + \eta \mathbf{v}) \approx E_{\text{in}}(\mathbf{w}_t) + \eta \mathbf{v}^T \nabla E_{\text{in}}(\mathbf{w}_t)
$$ 其中 $E_{\text{in}}(\mathbf{w}_t)$ 以及 $\nabla E_{\text{in}}(\mathbf{w}_t)$ 是已知的,$\eta$ 是正数,于是上式中最佳的 $\mathbf{v}$ 为:
$$\mathbf{v} = - \frac{\nabla E_{\text{in}}(\mathbf{w}_t)}{||\nabla E_{\text{in}}(\mathbf{w}_t)||}
$$ 于是迭代过程为
$$\mathbf{w}_{t+1} \leftarrow \mathbf{w}_{t} - \eta_1 \frac{\nabla E_{\text{in}}(\mathbf{w}_t)}{||\nabla E_{\text{in}}(\mathbf{w}_t)||}
$$ 这就是负梯度方向,因此在负梯度方向上 $E_{\text{in}}$ 下降最快。
choice of $\eta$
$\eta$ 的大小对 $E_{\text{in}}$ 优化的过程也有一定影响,如下图所示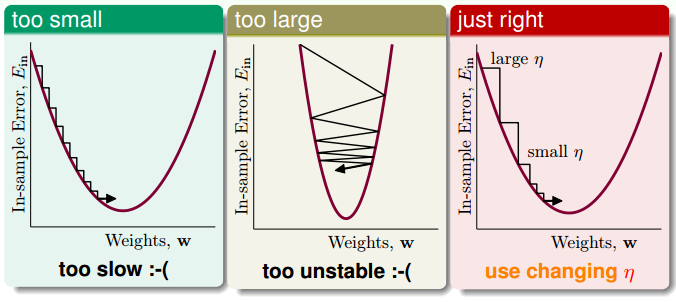
- $\eta$ 太小:优化速度太慢
- $\eta$ 太大:优化过程不稳定
因此比较合适的选择是,使 $\eta$ 随着 $||\nabla E_{\text{in}}(\mathbf{w}_t)||$ 变化,于是我们令 $$\eta_2 = \eta_1 \cdot ||\nabla E_{\text{in}}(\mathbf{w}_t)||
$$ 带入上面的式子,得到
$$\mathbf{w}_{t+1} \leftarrow \mathbf{w}_{t} - \eta_2 ||\nabla E_{\text{in}}(\mathbf{w}_t)|| $$
Logistic Regression Algorithm
综合上面的内容,我们得到了 Logistic Regression 算法,如图所示:
以上就是 Logistic Regression 算法的介绍。


