这一节主要介绍线性回归算法。
Linear Regression Problem
对于输出空间 $\mathcal{Y} = \Bbb{R}$ 的一类问题,一个比较简单的想法就是:将 Linear Classification 的决策函数中的 sign 函数去掉,使用各种特征的加权结果来表示 $y$
$$y \approx \sum_{i = 0}^{d} w_i x_i = \textbf{w}^T \textbf{x}$$ 这就是线性回归算法,它的假设空间为 $$h(\textbf{x}) = \textbf{w}^T \textbf{x}$$ 线性回归的目标是寻找一条直线 ($\Bbb{R}^2$) 或者一个平面 ($\Bbb{R}^3$)或者超平面($\Bbb{R}^n$),使得误差最小,常用的误差函数是平方误差 $$E_{in}(\textbf{w}) = \frac{1}{N} \sum_{n = 1}^{N} \left( h(\textbf{x}_n) - y_n \right)^2$$$$E_{out}(\textbf{w}) = \underset{(x,y) \sim P}{\epsilon} \Big( \textbf{w}^T \textbf{x} - y \Big)$$
Linear Regression Algorithm
将 $E_{in}$ 写成矩阵形式
$$
\begin{split}
E_{in}(\textbf{w}) &= \frac{1}{N} \sum_{n = 1}^{N} \left(h(\textbf{x}_n) - y_n\right)^2 \\
&= \frac{1}{N} \Bigg\Vert
\begin{matrix}
\textbf{x}_1^T \textbf{w} - y_1 \\
\textbf{x}_2^T \textbf{w} - y_2 \\
\cdot \cdot \cdot \\
\textbf{x}_N^T \textbf{w} - y_N \\
\end{matrix}
\Bigg\Vert^2 \\
&= \frac{1}{N} \Vert X \textbf{w} - \textbf{y} \Vert^2
\end{split}
$$
其中
$$
X = \Bigg[
\begin{matrix}
x_1^T, 1 \\
x_2^T, 1 \\
\cdot \cdot \cdot \\
x_N^T, 1 \\
\end{matrix}
\Bigg]
\in \Bbb{R}^{N \times (d+1)}
$$$$\textbf{w} \in \Bbb{R}^{(d+1) \times 1}$$$$\textbf{y} \in \Bbb{R}^{N \times 1}$$
我们的目标是找到一个 $\textbf{w}$,使得 $E_{in}(\textbf{w})$ 尽可能小。因此,将 $E_{in}(\textbf{w})$ 对 $\textbf{w}$ 求导,得到:
$$\nabla E_{in} (\textbf{w}) = \frac{2}{N} X^T(X\textbf{w} - \textbf{y})
$$令$\nabla E_{in}(\textbf{w}) = 0$,得到 $\textbf{w}$ 的最优解 $$\textbf{w}_{\text{LIN}} = \big( X^TX\big)^{-1}X^T\textbf{y}=X^{\dagger}\textbf{y}
$$ 其中 $$X^{\dagger}=\big(X^TX\big)^{-1}X^T
$$ 称为矩阵 $X$ 的伪逆,于是 $$h(\textbf{x}) = \textbf{w}_{\text{LIN}}^T \textbf{x}$$
将上面做一个小结,得到 Linear Regression 算法的流程如下:
Generalization Issue
下面我们来分析一下 Linear Regression 的 $E_{in}$
$$\begin{aligned}
E_{in}({w_{LIN}})&=\frac{1}{N}||{y-\hat{y}}||^2\\
&=\frac{1}{N}||y-XX^{\dagger}y||^2 \\
&=\frac{1}{N}||(I-H)y||^2 \\
\end{aligned}
$$ 其中 $H = XX^{\dagger}$ 是投影矩阵,把 $y$ 投影到 $X$ 的 $d+1$ 个向量构成的平面上,$H$ 有如下的性质:
- 对称性 $H=H^T$
- 幂等性 $H^2=H$
- 半正定性 $\lambda_i \geq 0$
- $trace(I-{H}) = N-(d+1)$
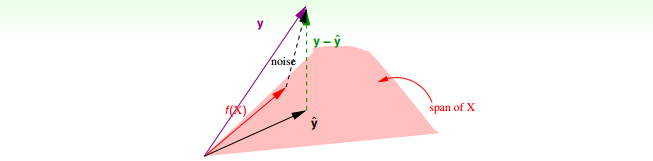
假设 $y = f(X) + \text{noise}, f(x) \in \text{span}$,那么如上图所示,有
$$\begin{aligned}
E_{in}({w_{LIN}})
&=\frac{1}{N}||(I-{H})y||^2 \\
&=\frac{1}{N}||(I-{H})noise||^2 \\
&=\frac{1}{N}trace(I-{H})||noise||^2 \\
&=\frac{1}{N}(N-(d+1))||noise||^2
\end{aligned}
$$ 得到:
$$E_{in}({w_{LIN}})=||noise||^2 \cdot \big( 1 - \frac{d+1}{N} \big)$$ $$E_{out}({w_{LIN}})=||noise||^2 \cdot \big( 1 + \frac{d+1}{N} \big)$$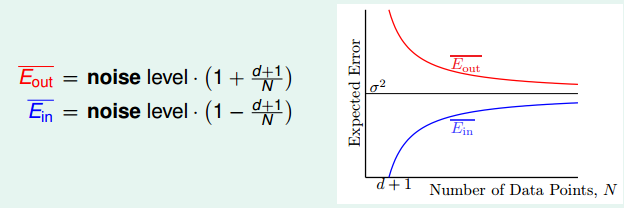
两者最终都向 $\sigma^2$ (noise level)收敛,差距是 $\frac{2(d+1)}{N}$,因此说明算法是可行的。
Linear Regression for Binary Classification
对比一下 Linear Classification 与 Linear Regression:
- Linear Regression
- 用于分类问题
- $\mathcal{Y} = \{ +1, -1\}$
- $h(\textbf{x})=\text{sign}(\textbf{w}^T\textbf{x})$
- NP-hard,难于求解
- Linear Regression
- 用于回归问题
- $\mathcal{Y} = \Bbb{R}$
- $h(\textbf{x})=\textbf{w}^T\textbf{x}$
- 易于求解
因为 $$\text{err}_{0/1} = \big[\big[ \text{sign}(\textbf{w}^T\textbf{x}) \neq y\big]\big] \leq \text{err}_{\text{sqr}} = (\textbf{w}^T\textbf{x} - y)^2
$$ 所以可以将 Linear Regression 用于分类问题上:
- run Linear Regression on binary classification data $\mathcal{D}$
- return $g(\textbf{x}) = \text{sign}(\textbf{w}_{\text{LIN}}^T\textbf{x})$
以上便是 Linear Regression 的内容。


