这一节主要讨论在有噪声的情况下,VC维理论是否仍适用。
Noise and Probabilistic Target
回顾之前提到的机器学习的流程图,学习的目的,就是找到一个函数 $g$,使得它与目标函数 $f$ 差不多。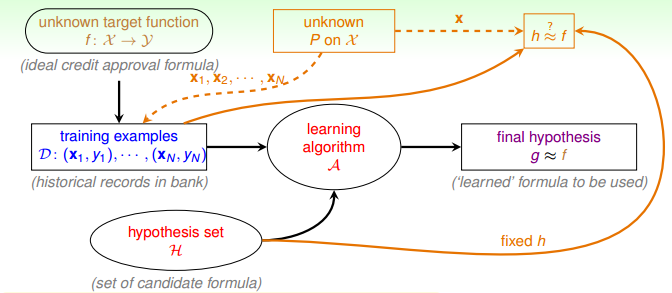
然而在现实生活中,往往伴随着噪声: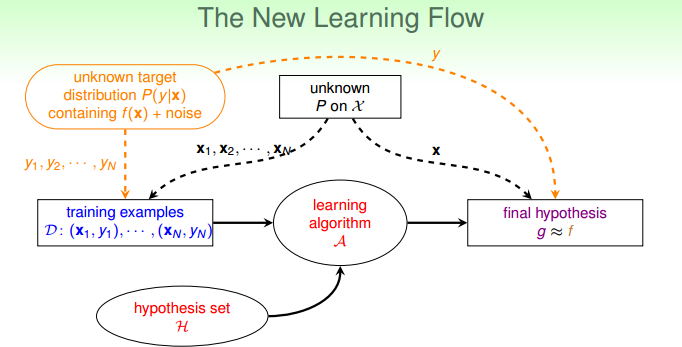
这些噪声的类别是多种多样的
- noise in $y$:如标签标错了
- noise in $x$:如原本的数据就存在噪声
没有噪音时,$x$ 服从同一个概率分布 $P$,$y=f(x)$ 是一个固定的值;有噪声时,$x$ 仍然服从同一个概率分布 $P$,$y \sim P(y|x)$ 不再是一个固定的值。
以之前提到的珠子为例子,珠子的两种颜色分别表示了 $h(x)$ 与 $f(x)$ 相等或者不等的情况。我们通过抽样,利用珠子属于某种颜色的频率来估计 $h(x) = f(x)$ 的概率。
在没有噪声的情况下,$y$ 是固定的,因此珠子的颜色是确定的。在有噪声的情况下,$y$ 不是固定的,因此珠子的颜色是变化的,此时我们仍然可以进行抽样的实验,只不过在进行统计的时候,我们记录的是珠子在抽出来那一刻的颜色。这样,我们就可以跟以前一样,通过频率来估计概率。
因此,只要 $x \sim P$ 并且 $y \sim P(y|x)$,也就是说 $(x,y) \sim P(x,y)$,VC维理论仍然适用。于是,学习的目的,从预测 $f$ 变成了预测 $p(y|x)$,其中 $p(y|x)$ 由 $f(x)$ 以及噪声构成。
对于 $f$,我们可以将其想象为分布 $P(y|x)$ 的一种特殊形式。
- $y = f(x)$时,$P(y|x) = 1$
- $y \neq f(x)$时,$P(y|x) = 0$
这样就可以将无噪声以及有噪声的情况统一起来,学习的流程图更新成以下形式:
Error Measure
我们需要有一个准则来衡量所选择的假设函数 $g$ 与目标函数 $f$ 相似程度,通常的方法是定义一个错误函数(也叫做代价函数) $E(g,f)$。
这个错误函数描述的是在整个样本空间(不只是训练样本)中,$g$ 与 $f$ 的相似程度,并且通常来讲,是 $g$ 与 $f$ 在每个样本点上的错误的平均。
$$E_{in}(g) = \frac{1}{N} \sum_{n=1}^{N} err \Big( g(x_n), f(x_n) \Big)$$$$E_{out}(g) = \underset{x \sim P}{\epsilon} err \Big( g(x_n), f(x_n) \Big)$$
常用的两种错误衡量方式 $err \big( g(x), f(x) \big) = err \big( \tilde{y}, y \big)$:
- 0/1 error for classification:$err \big( \tilde{y}, y \big) = \big[ \tilde{y} \neq y \big] $
- squared error for regression:$err \big( \tilde{y}, y \big) = \big( \tilde{y} - y \big) ^ 2 $
错误衡量准则会对学习过程起到指导作用,因此对于同一个问题,使用不同的错误衡量准则,得到的结果可能不一样。
对机器学习流程图进一步修改,加入了错误衡量的模块,该模块对算法和最终的假设选择都起着很大影响。
Algorithmic Error Measure
在现实中,要设计出真正的错误衡量有时候会很困难,在设计错误衡量方式时,常常使用替代的方式 $\hat{err}$:
- 有意义的错误衡量
例如 0/1 error,表示的是 flipping 的噪声,如果 0/1 error 很小,说明出错的样本数很少;
例如 squared error,表示的是噪声是高斯的分布,如果 squared error 很小,说明高斯噪声很少; - 对设计算法容易的错误衡量
例如有闭式解的算法对应的错误衡量方式;
例如具有凸函数性质的错误衡量方式。
于是,学习的流程图改为下面的形式,其中 $err$ 表示的是真正的错误衡量方式,而$\hat{err}$ 表示的是我们用在算法中的错误衡量方式,我们使用 $\hat{err}$ 来替代 $err$ 进行算法中的优化以及假设函数的选择。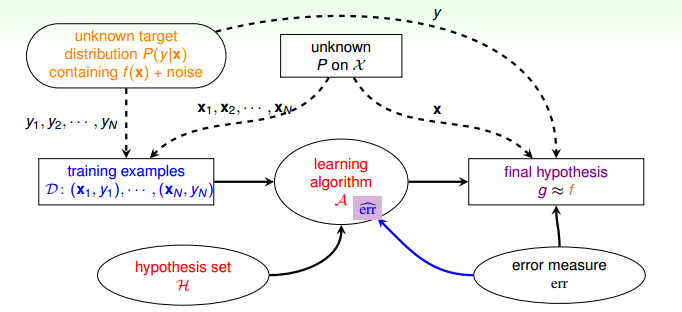
Weighted Classification
我们可以使用 cost matrix 表示 0/1 error
其中 false reject 表示的是把 $y=+1$ 预测为 $y=-1$,false accept 表示的是把 $y=-1$ 预测为 $y=+1$。
当这两类错误的 cost 相等时,表示这两类错误的重要性一致,当这两类错误的 cost 不相等时,表示其中一种错误更加严重,代价更高。
于是我们可以根据实际的需要,赋予两种错误不同的代价,这叫做 weighted classification。
下面是一个 cost matrix 的例子,在这个例子中,把 $y=+1$ 预测为 $y=-1$ 的代价是 $1$,而把 $y=-1$ 预测为 $y=+1$ 的代价是 $1000$,因此算法会惩罚后一种错误分类的情况。
通过改变样本的数目,可以将 weighted classification 转化为一般的 classification。用上一个例子来说明,我们可以将数据集中 $y=-1$ 的样本复制 1000 份,这样就相当于在没有加权的 0/1 error 下进行实验。于是可以使用之前用于 0/1 error 的算法,比如 pocket 算法。
将上面 cost matrix 的转化嵌入到算法中,便得到了 weighted pocket 算法


