接着上一篇所讨论的问题,继续讨论。
Recap and Preview
回顾一下机器学习的流程图:
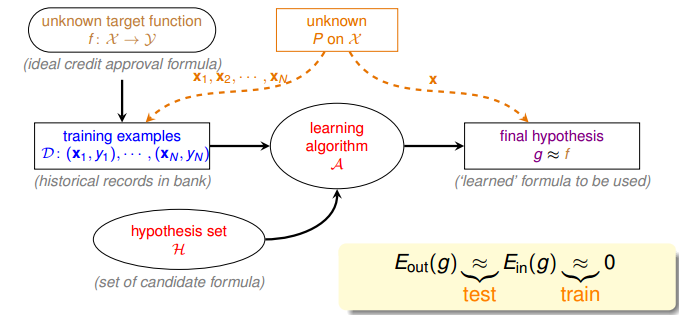
机器学习可以理解为寻找到 $g$,使得 $g \approx f$,也就是 $E_{out}(g) \approx 0$ 的过程。
为了完成这件事情,有两个关键的步骤:
- 保证 $E_{out}(g) \approx E_{in}(g)$,由 “训练” 过程来完成
- 保证 $E_{in}(g) \approx 0$,由 “验证” 过程来完成
当这两件事情都得到保证之后,我们就可以得到 $E_{out}(g) \approx 0$,于是完成了学习。
$M$ 的取值(hypothesis 的数目)会影响上面说的两个步骤:
- $M$ 太小,能保证 $E_{out}(g) \approx E_{in}(g)$,但是不能保证 $E_{in}(g) \approx 0$
(因为可选择的 hypothesis 的数目太少); - $M$ 太大,能保证 $E_{in}(g) \approx 0$,但是不能保证 $E_{out}(g) \approx E_{in}(g)$$\big(\begin{split}
\Bbb{P}_{\mathcal{D}}[BAD\ \mathcal{D}]
\le2M\exp(-2\epsilon^2N)
\end{split}
\big)$。
因此需要想办法解决 $M$ 较大时,$E_{out}(g) \approx E_{in}(g)$ 的问题。
Effective Number of Lines
由上一篇文章我们知道:
$$\Bbb{P} \Big[\Big| E_{in}(g) - E_{out}(g) \Big| > \epsilon\Big] \le 2M \exp(-2 \epsilon^2 N)$$
对于这个式子,$M = \infty$ 时,右侧的值很大,$E_{out}(g) \approx E_{in}(g)$ 不能保证。我们的想法是:尝试用一个合适的数 $m_H$ 代替式子中的 $M$,使无穷变成有限,如下式:
$$\Bbb{P} \Big[\Big| E_{in}(g) - E_{out}(g) \Big| > \epsilon\Big] \stackrel{?}{\le} 2 \cdot m_{\mathcal{H}} \cdot \exp(-2 \epsilon^2 N)$$
第一个式子中的 $M$ 来源于 “Union Bound”
$$\Bbb{P} [ \mathcal{B}_{1} \hphantom{1} or \hphantom{1} \mathcal{B}_{2} \hphantom{1} or \dots \mathcal{B}_{M} ] \le \Bbb{P} [ \mathcal{B}_{1}] + \Bbb{P} [ \mathcal{B}_{2}] + \dots + \Bbb{P} [ \mathcal{B}_{M}]$$
其中 $\Bbb{P}[\mathcal{B}_{M}]$ 表示的是第 $M$ 个假设函数 $h_M$ 在数据集上发生坏事情(即存在 BAD DATA,$E_{out}(h_M) \neq E_{in}(h_M)$)的概率。
然而当 $M$ 很大时,假设集中存在许多相似的假设函数 $h$,它们发生坏事情的概率和情形都很接近,这样使用 “Union Bound” 来计算整个假设集发生坏事情的概率,便存在许多重复的地方,于是算出来的概率会比实际的高很多(over-estimating)。
我们换一种思路,从数据点的分类结果来对假设集进行分类,这样就避免了假设之间相互重合的问题。以二元分类来阐述怎么解决这个问题:我们根据分类结果,对 $h$ 进行分类。
| 样本点大小 $N$ | 假设集 $H$ 等价类(考虑最多的情况) |
|---|---|
| 1 | 2 类:$\{o\}$、$\{x\}$ |
| 2 | 4 类:$\{oo\}$、$\{ox\}$、$\{xo\}$、$\{xx\}$ |
| … | … |
| N | $2^{N} 类$ |
对于一个大小为 $N$ 的数据集,任意一个假设函数 $h$ 都属于上述 $2^N$ 个等价类之间的一个,因此我们可以用 $2^N$ 来代替原不等式中的 $M$。
Effective Number of Hypotheses
我们把上面提到的等价类的概念起一个名字叫做 Dichotomy。
具体的 Dichotomy 的 size 与这 $N$ 个数据的具体取值有关(但是不会大于 $2^N$),为方便讨论我们取最大那个 size 来分析,取名为 growth function,记作 $m_\mathcal{H}(N)$,意思是假设空间在 $N$ 个样本点上能产生的最大二分数量。
$$m_\mathcal{H}(N) = \max \limits_{\textbf{x}_1,\textbf{x}_2,…,\textbf{x}_N \in \mathcal{X}} \big| \mathcal{H}(\textbf{x}_1,\textbf{x}_2,…,\textbf{x}_N) \big|$$
接下来我们需要计算 $m_\mathcal{H}(N)$,首先考虑几种不同的模型的 $m_\mathcal{H}(N)$
Positive Rays
确定一个点,规定在这个点的正方向为正,即 $h(x)=+1$,反方向为负,即 $h(x)=-1$。在这种情况下 $m_\mathcal{H}(N) = N + 1$,如下图所示。
Positive Intervals
确定两个点,规定在这两个点之间为正,即 $h(x)=+1$,两个点之外为负,即 $h(x)=-1$。在这种情况下 $m_\mathcal{H}(N) = {N+1 \choose 2} + 1$,如下图所示。
Convex Sets
顶点在同一个圆上的凸多边形,规定圆上与多边形相交的点为正,即 $h(x)=+1$,没有与多边形相交的点为负,即 $h(x)=-1$。在这种情况下 $m_\mathcal{H}(N) = 2^N$,如下图所示。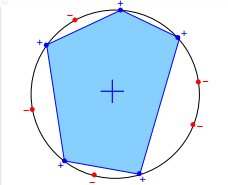
2D perceptrons
就是前面举的平面上的点分类的例子,某些情况下 $m_\mathcal{H}(N) < 2^N$。
将上面几种情况总结如下:
| model | $m_\mathcal{H}(N)$ |
|---|---|
| Positive Rays | $m_\mathcal{H}(N) = N + 1$ |
| Positive Intervals | $m_\mathcal{H}(N) = {N+1 \choose 2} + 1$ |
| Convex Sets | $m_\mathcal{H}(N) = 2^N$ |
| 2D perceptrons | $m_\mathcal{H}(N) < 2^N$ in some case |
Break Point
我们希望 $m_H(N)$ 是多项式形式而不是指数形式的,这样当 $N$ 很大的时候,不等式右边趋近于0,才能保证 $E_{out}(g) \approx E_{in}(g)$:
$$\Bbb{P} \Big[\Big| E_{in}(g) - E_{out}(g) \Big| > \epsilon\Big] \stackrel{?}{\le} 2 \cdot m_{\mathcal{H}} \cdot \exp(-2 \epsilon^2 N)$$
因此,将 $m_{\mathcal{H}}$ 替换为 $2^N$ 还不够,为此我们引入一个概念叫 break point,定义如下
- if no $k$ inputs can be shattered by $\mathcal{H}$, call $k$ a break point for $\mathcal{H}$
- $m_{\mathcal{H}}(k) < 2^{k}$
- $k+1$, $k+2$, $k+3$, $…$ also break points
- will study minimum break point $k$
对应的,上面所提到的四种模型的 break point 如下:
| model | $m_\mathcal{H}(N)$ | break point |
|---|---|---|
| Positive Rays | $m_\mathcal{H}(N) = N + 1$ | break point at 2 |
| Positive Intervals | $m_\mathcal{H}(N) = {N+1 \choose 2} + 1$ | break point at 3 |
| Convex Sets | $m_\mathcal{H}(N) = 2^N$ | no break point |
| 2D perceptrons | $m_\mathcal{H}(N) < 2^N$ in some case | break point at 4 |
我们猜测 $m_\mathcal{H}(N)$ 与 break point 有下面的关系:
- no break point:$m_\mathcal{H}(N) = 2^N$
- break point $k$:$m_\mathcal{H}(N) = O(N^{k-1})$
如果猜测成立,那么在有 break point 的情况下,$m_H(N)$ 便是一个多项式形式,这样就能保证 $E_{out}(g) \approx E_{in}(g)$ 了。
因此,接下来我们需要探讨,break point 与 $m_\mathcal{H}(N)$ 之间的关系,我们将在下几篇文章中对此进行讨论。


