在这篇文章中,我们主要探讨,机器到底能不能进行学习这个问题。
Learning is Impossible?
从前面的文章中,我们已经知道,机器学习的过程,就是通过现有的训练集 $D$ 学习,得到预测函数 $h$,并且使得它接近于目标函数 $f$。
我们必须思考的问题是:
这种预测是可能的么?也就是说,机器能通过学习得到 $h$,使得 $h \approx f$ 吗?
No free lunch
机器学习领域有一个著名的理论,叫做 “没有免费的午餐” 定理(No Free Lunch Theorem, 简称 NFL 定理)。用比较通俗易懂的话来讲,意思就是说:“学习” 可能是做不到的。
在训练样本集(in-sample)中,可以求得一个最佳的假设 $g$,该假设最大可能的接近目标函数 $f$,但是在训练样本集之外的其他样本(out-of-sample)中,假设 $g$ 和目标函数 $f$ 可能差别很远。
Example
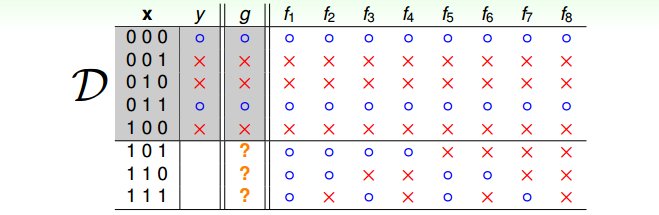
我们举一个例子来说明上面这段话的意思。现在假设有这样一个数据集 $X=\{000,001,…,111\}$ 总共8个数据,使用函数 $f$ 对数据集中的每一个数据分类(圈或叉)。现在我们手头有5个训练样本,我们想让机器使用这些训练样本学习到函数$f$。
由于机器只能看到训练集的样本(5个),因此它能学习得到函数 $g$,使得在这些训练样本上,$g$ 与 $f$ 的预测结果一样。
但是,因为机器看不见训练集外的样本(剩下的3个),对于这些样本,机器只能自己猜测$g(x)$的值。而无论机器预测的结果是怎么样的,我们总能够找到$f$,使得在这些训练集外的样本上,$g \neq f$。
Summary
从上面的例子我们可以看出,机器能学习的,只是它看得见的样本(in-sample),而对于它看不见的样本(out-of-sample),学习效果就很难保证了。
如果是这样子的话,机器学习的作用的很有限了,毕竟我们更需要的,是机器机帮我们处理没见过的数据。
嗯,事情一定没这么简单。
Probability to the Rescue
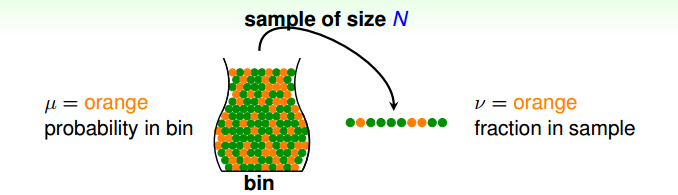
我们想象这样一个场景:有一个罐子,这个罐子里装有橙色和绿色两种颜色的珠子,我们如何在不查遍所有珠子的情况下,得知罐子中橙子珠子所占的比例呢?一个想法就是使用抽样的方法,通过频率来预测概率。
假设罐子中橙色珠子的概率为 $\mu$(未知),则绿色珠子的概率为 $1-\mu$;假设通过抽样查出的橙色珠子比例为 $v$(已知),则绿色珠子的比例为 $1-v$。那么我们可不可以通过 $v$ 来预测 $\mu$ 呢?
Hoeffding’s inequality
数学上有个霍夫丁不等式,专门回答了这个问题。这个不等式是这样子的:
当样本数量 $N$ 足够大时,$v$ 和 $\mu$ 有如下关系:
$$\Bbb{P}[\left|\nu-\mu\right|\gt\epsilon]\le2\exp\big(-2\epsilon^2N\big)$$
从上面的式子可以看出,随着样本数量 $N$ 的逐渐增大,$v$ 与 $\mu$ 接近的概率也逐渐增大,因此可以说 $v$ 与 $\mu$ 大概近似相等(probably approximately correct,PAC),因此,选择合适的 $N$ 以及 $\epsilon$,就可以通过 $v$ 预测 $\mu$。
Connection to Learning
我们可以将以上的情景与机器学习问题对应起来,如下图所示:

相对应的概念如下所示:
- 罐子:数据集,包括 in-sample 以及 out-of-sample
- 橙色珠子:数据 $x_n$, 其中 $h(x_n) \neq f(x_n)$
- 绿色珠子:数据 $x_n$, 其中 $h(x_n) = f(x_n)$
- 橙色珠子概率 $\mu$:$h(x) \neq f(x)$ 的概率
- 抽到的珠子:训练样本(我们看得到的那些)
- 抽到橙色珠子:在某个样本点 $x_n$ 上,$h(x_n) \neq f(x_n) = y_n$
- 抽到绿色珠子:在某个样本点 $x_n$ 上,$h(x_n) = f(x_n) = y_n$
- 橙色珠子频率 $v$:$h(x) \neq f(x)$ 的频率
- 抽样动作:判断 $h(x_n)$ 与 $f(x_n)=y_n$ 是否相等
于是在样本数足够多的情况下,我们可以通过测试 $h(x_n) \neq y_n$ 的频率来推断 $h(x) \neq f(x)$ 的概率。这里需要注意的是,$x_n$ 需要是独立同分布的,但是我们并不需要知道具体的分布函数是什么。
Learning Flow
我们对学习流程图进行完善,如下图所示:
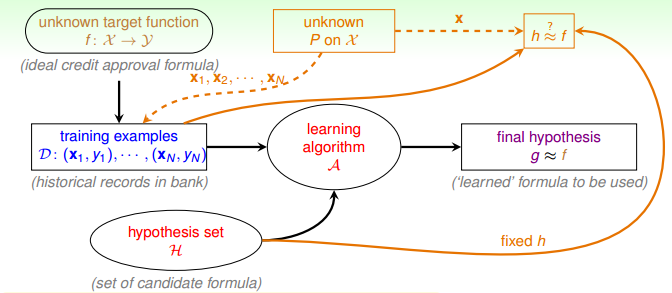
我们在流程图中增加了一个数据的分布函数 $P$,我们并不知道这个分布具体的样子(但是没关系),我们利用这个分布进行抽样,产生训练样本,同时利用这些训练样本,计算 $h(x) \neq f(x)$ 的频率 $E_{in}(h)$,并且使用这个频率来估计 $h(x) \neq f(x)$ 的概率 $E_{out}(h)$。这里所说的 $h$,是我们从假设集 (hypothesis set) 中选择的一个特定的 $h$。

The Formal Guarantee
将霍夫丁不等式中的 $\mu$ 换成 $E_{out}(h)$,$v$ 换成 $E_{in}(h)$,就可以得到下面的式子:
$$\Bbb{P}\left[\left|E_{in}(h)-E_{out}(h)\right|\gt\epsilon\right]\le2\exp\big(-2\epsilon^2N\big)$$
上面的公式保证了在一定条件下,$E_{in}(h)$ 与 $E_{out}(h)$ 不会相差太远,那么只要我们能选择合适的 $h$ 使得 $E_{in}(h)$ 比较小,那么 $E_{out}(h)$ 也会比较小。
Verification of One $h$
整理一下,对于一个固定的 $h$,霍夫丁不等式告诉我们,在样本数足够多的情况下,如果 $E_{in}(h)$ 很小,那么 $E_{out}(h)$ 也会大概率比较小。
机器学习要做的事,是通过算法 $\mathcal{A}$ 从假设集 $H$ 中选择 $g$,使得 $g$ 尽可能接近 $f$。换句话来讲,需要在假设集 $H$ 中找到一个 $h$,使得 $E_{in}(h)$ 很小,然后把 $h$ 当成最终的预测函数 $g$。
我们现在做的事情,因为只涉及了一个 $h$,准确来讲不是 “学习”,而是 “验证”,即对于一个 $h$,通过 $E_{in}(h)$ 估计 $E_{out}(h)$。
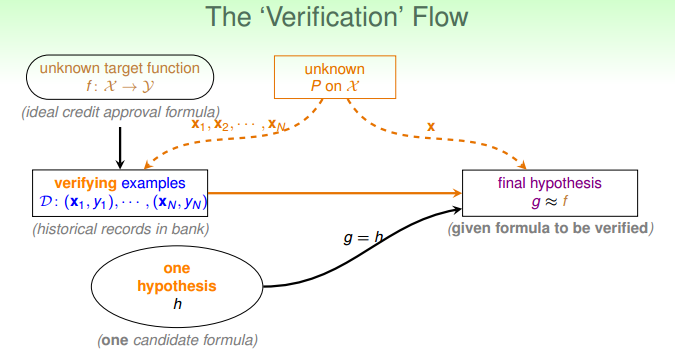
我们还需要探讨,如果算法是在多个 $h$ 中进行选择(而不是只有一个 $h$,不需要选择),那么情况有什么变化。也就是从探讨 $E_{in}(h)$ 与 $E_{out}(h)$ 的关系,变成探讨 $E_{in}(g)$ 与 $E_{out}(g)$ 的关系。
Connection to Real Learning
首先我们考虑假设集中的假设是有限多个的情况。
来看一下下面这个表格,表格中的每一行表示一个固定的 $h$ 的情况,表格中的每一列表示一笔数据集,表格里的 “BAD” 表示,在这笔数据集上,对于某个特定的 $h$,$E_{in}(h)$ 与 $E_{out}(h)$ 相差很大,我们把这样的数据叫做是这个 $h$ 上的 BAD data。
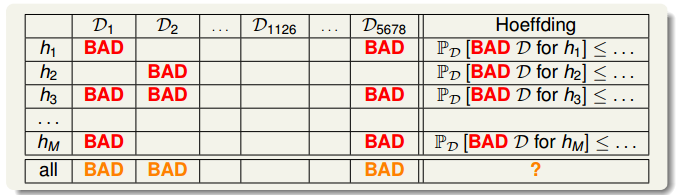
霍夫丁不等式告诉我们,对于一个固定的$h$,出现 $E_{in}(h)$ 与 $E_{out}(h)$ 相差很大的概率很小,也就是说,对于表格中的每一行, BAD data 出现的概率很小,在这样的情况下,我们才能通过 $E_{in}$ 来预测 $E_{out}$。
$$
\Bbb{P}\big[ \big| E_{in}(h) - E_{out}(h) \big| > \epsilon \big] \le 2 \exp \big( -2 \epsilon^2 N \big)
$$
同样的,当有多个 $h$ 可选择时,我们也希望 BAD data 出现的概率小,这样才能让算法在假设集中自由选择 $h$,保证能通过$E_{in}$ 来预测 $E_{out}$。
这种情况下,只要数据对于某个 $h$ 而言是 BAD data,它在这个假设集中就是 BAD data,其出现的概率为:
$$
\begin{split}
\Bbb{P}_{\mathcal{D}}[BAD\ \mathcal{D}]
&=\Bbb{P}_{\mathcal{D}}[BAD\ \mathcal{D}\ for\ h_1\ or\ BAD\ \mathcal{D}\ for\ h_2\ or\ …\ or\ BAD\ \mathcal{D}\ for\ h_M]\\
&\le\Bbb{P}_{\mathcal{D}}[BAD\ \mathcal{D}\ for\ h_1]+ \Bbb{P}_{\mathcal{D}}[BAD\ \mathcal{D}\ for\ h_2]+ …+\Bbb{P}_{\mathcal{D}}[BAD\ \mathcal{D}\ for\ h_M]
\\
&\le2\exp\big(-2\epsilon^2N\big)+\exp\big(-2\epsilon^2N\big)+\exp\big(-2\epsilon^2N\big)+…+\exp\big(-2\epsilon^2N\big)\\
&=2M\exp\big(-2\epsilon^2N\big)
\end{split}
$$其中 $M$ 表示的是假设集中 $h$ 的个数。
因此得到结论:如果 $M$ 的值是有限的,在 $N$ 足够大的情况下,BAD data 出现的概率很小,即无论哪个 $h$,都有 $E_{in}(h) \approx E_{out}(h)$ (PAC),那么我们通过合适的算法选择一个 $E_{in}$ 小的 $h$,就能保证 $E_{out}$ 小(PAC),于是学习成功了。
最后完善学习流程图:
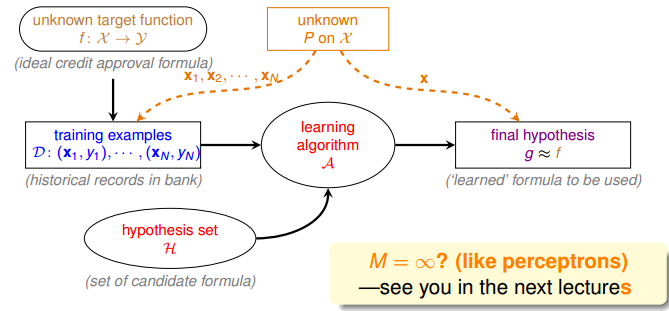
以上,我们讨论了假设集中的假设是有限多个的情况下,$E_{in}(g)$ 与 $E_{out}(g)$ 的关系。关于假设集中的假设是无限多个的情况,将在接下来的文章中讨论。


