这节课主要介绍感知器算法(Perceptron Learning Algorithm)。
Perceptron Hypothesis Set
对于一个线性可分的二分类问题,我们可以采用感知器 (Perceptron)这种假设集。
采用这种假设集进行分类的思想是这样的:
我们假设样本的类别是由样本每一个特征 $\textbf{x}_i$ 共同决定,其中不同的特征的重要程度不一样。于是我们通过对所有的特征进行加权 $\sum_{i=1}^d \textbf{w}_i \textbf{x}_i$,得到一个“分数”,将这个“分数”与一个阈值 $threshold$ 进行比较,如果“分数”大于阈值,那么这个样本属于一个类别(类别“+1”),如果“分数”小于阈值,那么这个样本属于另一个类别(类别“-1”)。
这种模型可以用下面的表达式表示出来:
$$
\begin{split}
h(\textbf{x})
&= sign \Bigg( \Big( \sum_{i=1}^d \textbf{w}_i \textbf{x}_i \Big) - threshold \Bigg) \ \ \ \ h\in \mathcal{H} \\
&= sign \Bigg( \Big( \sum_{i=1}^d \textbf{w}_i \textbf{x}_i \Big) + \Big(- threshold \Big) \cdot \Big( +1 \Big) \Bigg) \\
&= sign \Big( \sum_{i=0}^d \textbf{w}_i \textbf{x}_i \Big) \\
&= sign \Big( \textbf{w}^T \textbf{x} \Big)
\end{split}
$$
其中不同的向量 $\textbf{w}$ 代表了不同的假设函数 $h(\textbf{x})$,我们的目标是使用一些算法调整 $w$ 的值,使得假设函数 $h(\textbf{x})$ 与我们要预测的函数 $f(\textbf{x})$ 尽可能的接近。
我们的想法是:如果 $h(\textbf{x})$ 与 $f(\textbf{x})$ 足够接近,那么它们作用在训练集 $D$ 上的结果会是一样的,即对训练集中的 $\textbf{x}$,有 $f(\textbf{x}) = h(\textbf{x})$。反过来说,如果对所有训练集中的 $\textbf{x}$,有 $f(\textbf{x}) = h(\textbf{x})$,那么在一定程度上,我们可以认为 $h(\textbf{x})$ 与 $f(\textbf{x})$ 是接近的。
Perceptron Learning Algorithm (PLA)
这个模型中训练 $\textbf{w}$ 的算法称为感知器算法(Perceptron Learning Algorithm),算法的思想是(尽可能地)对预测错误的样本进行修正,使得分类器的预测结果越来越好。预测错误的样本可以分为以下两种类型:
当 $f(\textbf{x})=y=+1$ 而预测结果 $h(\textbf{x})=sign(\textbf{w}^T\textbf{x})=-1$ 时,说明此时 $\textbf{w}$ 与 $\textbf{x}$ 的内积过小,夹角过大,需要让 $\textbf{w}$ 靠近 $\textbf{x}$,因此将 $\textbf{w}$ 改为 $\textbf{w}+\textbf{x}=\textbf{w}+y\textbf{x}$;
当 $f(\textbf{x})=y=-1$ 而预测结果 $h(\textbf{x})=sign(\textbf{w}^T\textbf{x})=+1$ 时,说明此时 $\textbf{w}$ 与 $\textbf{x}$ 的内积过大,夹角过小,需要让 $\textbf{w}$ 远离 $\textbf{x}$,因此将 $\textbf{w}$ 改为 $\textbf{w}-\textbf{x}=\textbf{w}+y\textbf{x}$;
反复修正预测错误的样本点直到所有训练样本都预测正确,选择预测错误的样本的顺序没有限制,可以按自然顺序,也可以随机选择。
算法描述如下图:

例子
我们举一个例子来说明 PLA 算法的过程。




Guarantee of PLA
目前我们还有一些问题没有讨论,其中比较重要的一个问题是,PLA是不是收敛的,即算法最终能不能停止下来。
首先我们讨论线性可分的情况,线性不可分的情况在下一节中讨论。当数据集是线性可分时,表示存在 $\textbf{w}_f$ 使得 $y_n = sign(\textbf{w}_f^T \textbf{x}_n)$,下面证明PLA是收敛的,即 $\textbf{w}$ 能收敛到 $\textbf{w}_f$,即算法能停止下来。
- $\textbf{w}_f$ 与 $\textbf{w}_t$ 的内积会单调递增

- $\textbf{w}_t$ 的长度有限制

以上两点可以推出:
当算法从 $\textbf{w}_0 = 0$ 开始时,算法更新次数 $T \leq \frac{R^2}{\rho^2}$
其中 $$R^2 = \max \limits_{n}\{f(\textbf{x})\}$$$$ \quad \rho = \min \limits_{n} y_n \frac{\textbf{w}_f^T}{||\textbf{w}_f^T||} \textbf{x}_n$$
因此说明了算法最终会收敛。
总结
我们对PLA进行一下总结:
收敛性
在数据是线性可分的条件下,算法能收敛。
算法的优点
算法容易简单、实现;
算法速度快;
在任意维度下都能工作。
算法的缺点
需要数据是线性可分的条件;
不知道算法什么时候收敛。
Non-Separable Data
当数据集是线性不可分时,表示数据中有噪声(这里的噪声是相对于感知器这个假设集而言的)。在这种情况下,学习的过程发生了一点改变: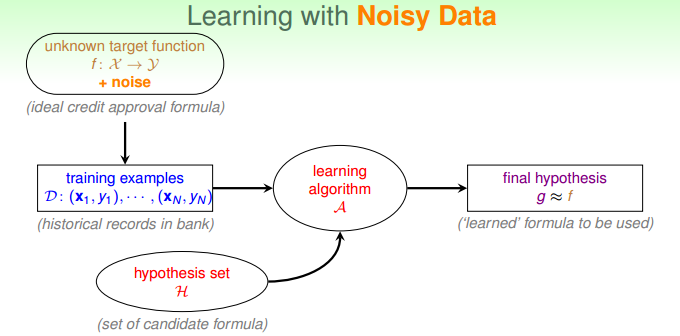
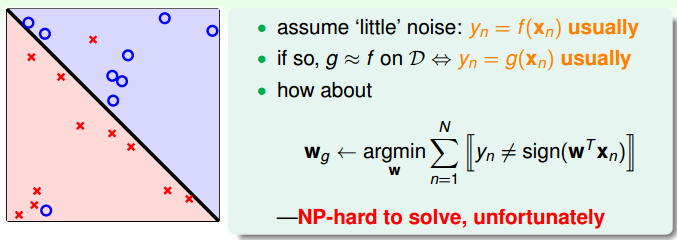
对感知器模型来说,此时可能无法使所有样本都正确分类,此时我们应该退而求其次,找尽可能犯错少的分界面,我们的学习的目标从
$$ \arg \limits_{ \textbf{w} } y_n = sign( \textbf{w}^T \textbf{x}_n) $$ 变成了
$$ \arg \min \limits_{w} \sum {[[y_n \neq sign(w^Tx_n)]]}$$不幸的是,这是一个 NP-hard 问题。
此时的一种思路是使用贪心算法,于是PLA可以改进成Pocket算法:


